a transmisión de señales sin alambre no se realiza mediante cambios en las corrientes eléctricas sino variando la radiación electromagnética. En resonancia magnética la radiación no se transmite de manera continua sino fragmentada en pulsos. Estos pulsos se pueden agrupar en diferentes secuencias de pulsos.
La forma de los pulsos es fundamental para alcanzar el objetivo propuesto. Existen pulsos selectivos que se utilizan para crear un solo corte del objeto de estudio y pulsos no selectivos que pueden excitar el objeto en su totalidad; son los que utilizaremos para obtener imágenes tridimensionales.
La figura 01-08 muestra un pulso fuerte, que no tiene especial relevancia en la imaginería por resonancia magnética. Para mejorar la calidad y aplicabilidad de los pulsos es necesario darles forma, es decir, variar su amplitud en función del tiempo (Figuras 01-08 y 01-09). Las formas de pulso más ampliamente utilizadas son la Gaussiana y la sinc, obteniéndose con esta última un mejor perfil de corte.
El pulso sinc se define mediante la ecuación: sinc (x) = sin (x)/x
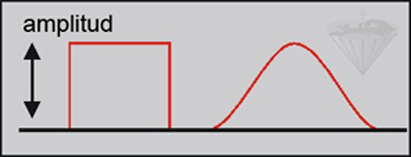
Figura 01-08:
Pulso fuerte (izquierda) y pulso formado (derecha).
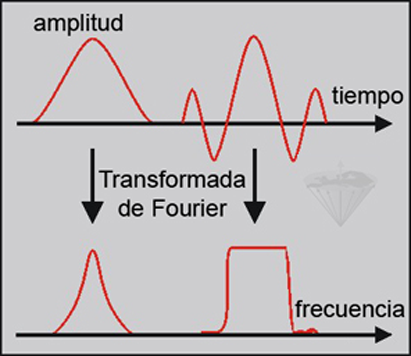
Figura 01-09:
Pulsos Gaussiano (izquierda) y sinc (derecha). Mientras que la transformada de Fourier del pulso Gaussiano conduce a una forma Gaussiana, la transformada Fourier del pulso sinc lleva a una forma casi rectangular. Esto es más conveniente en la IRM porque permite una mejor definición de un corte a través del cuerpo humano.
El ancho de banda es la gama de frecuencias que se incluyen en el pulso. Para cualquier señal es necesario definir un ancho de banda determinado. En general el ancho de banda es directamente proporcional a la cantidad de datos transmitidos o recibidos por unidad de tiempo. En los sistemas analógicos el ancho de banda se define como la diferencia entre la componente de señal de más alta frecuencia y la componente de señal de frecuencia más baja.
Una señal de voz típica tiene un ancho de banda de aproximadamente tres kilohercios (3 kHz); una señal de video transmitida por una televisión analógica (TV) tiene un ancho de banda de seis megahercios (6 MHz), unas 2.000 veces mayor que la señal de voz.
Las señales, como por ejemplo los pulsos de radiofrecuencia (RF), tienen una forma de onda determinada. Varían con el tiempo: son una función dependiente del tiempo. Sin embargo, podría ser más fácil y mejor trabajar y analizar las propiedades del pulso con respecto a la frecuencia de sus componentes.
Esta conversión se puede lograr mediante una Transformada de Fourier (TF). Las matemáticas que explican la TF son complejas pero, para nuestros propósitos, bastará con conocer el resultado de su utilización.
Mientras que la transformada de Fourier de un pulso gaussiano es también Gaussiana, la TF de un pulso sinc se aproxima al perfil rectangular ideal de un corte (Figura 01-09). Sin embargo, tampoco este tipo de pulso es el ideal para ser utilizado en todas las secuencias de RM, por lo que se han desarrollado una gran variedad de alternativas.
|
|
|---|