e todos los núcleos de la tabla periódica, ¹H, ¹³C, ¹⁹F, ²³Na, y ³¹P se encuentran entre los más interesantes para la imaginería por resonancia magnética. Todos ellos se producen de forma natural en el cuerpo. El protón de hidrógeno (¹H) es el más frecuentemente utilizado debido a que los dos componentes principales del cuerpo humano (agua y grasa) contienen hidrógeno. Todos estos núcleos tienen propiedades magnéticas que los distinguen de los isótopos no magnéticos.
Núcleos como ¹²C y ¹⁶O, que tienen números pares de protones y neutrones, no producen señales de resonancia magnética.
¹H consta de un solo protón de carga positiva que gira alrededor de su eje. Las partículas cargadas que giran sobre si mismas crean un campo electromagnético equivalente al que nace de un imán convencional (Figura 02-02).
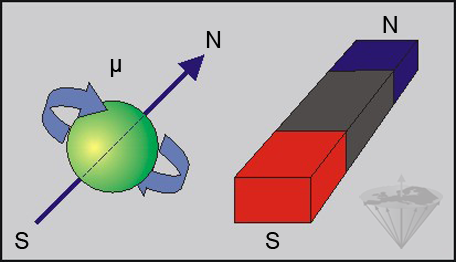
Figura 02-02:
Una partícula cargada girando sobre si misma posee un momento magnético μ característico y puede describirse como un dipolo magnético que crea un campo magnético similar al de un imán de barra.
(N = norte, S = sur).
Cuando núcleos atómicos con propiedades magnéticas se colocan en un campo magnético pueden absorber ondas electromagnéticas con frecuencias características. La frecuencia exacta depende del tipo de núcleo, la intensidad de campo y el entorno físico-químico del núcleo (Figura 02-03).
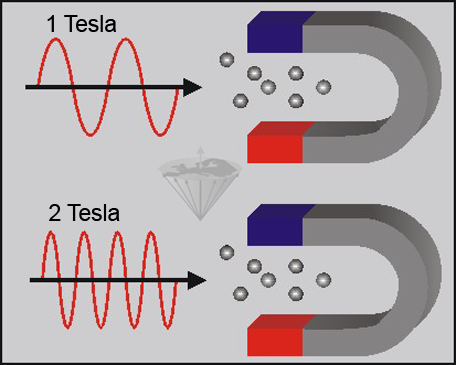
Figura 02-03:
Los núcleos serán capaces de absorber ondas electromagnéticas tanto en campos magnéticos fuertes como en los débiles. Sin embargo, la absorción se produce a una frecuencia que depende de la fuerza del campo, que es mayor en el campo magnético fuerte que en el débil.
En equilibrio observamos una población ligeramente mayor en el nivel de energía más bajo, produciéndose así magnetización. Para observar esta diferencia de población tenemos que transmitir una cantidad de energía igual a ΔE (la diferencia de energía entre los dos niveles).
La absorción y la reemisión de estas ondas de radio es el fenómeno básico utilizado en la IRM y la espectroscopia de RM. Para entender el fenómeno de resonancia magnética podemos utilizar dos paralelismos simples con fenómenos macroscópicos:
En primer lugar vamos a observar el comportamiento de una pequeña aguja magnética colocada en un campo magnético (Figura 02-04). Si la aguja es capaz de girar libremente ésta se orienta con respecto al campo de tal manera que se alcanza una situación de equilibrio. Este equilibrio se puede mantener indefinidamente si no hay fuerzas externas que influyan en el sistema.
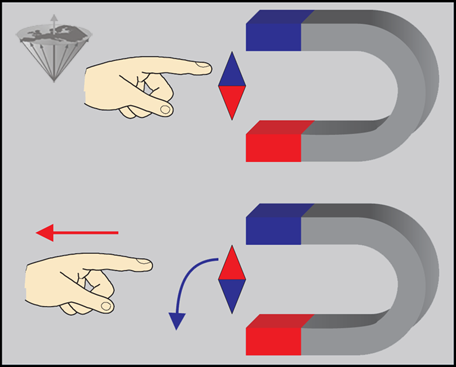
Figura 02-04:
Una aguja colocada en un campo magnético buscará un estado de equilibrio estable.
(Arriba) Al girar la aguja con un dedo, se le introduce energía y estará en una posición inestable rica en energía.
(Abajo) Tan pronto el dedo se retire, la aguja volverá a su estado estable.
Un segundo ejemplo ilustra la influencia de la tensión externa sobre la frecuencia de la onda absorbida o reemitida por el sistema: imagínese tres cuerdas de guitarra idénticas expuestas a tensiones diferentes: la superior no tiene tensión alguna, la del centro tiene tensión débil y la inferior tiene alta tensión. Si se excitan las cuerdas la vibración resultante es dependiente de la tensión de las cuerdas (Figura 02-05).
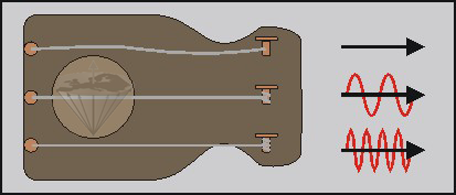
Figura 02-05:
Una cuerda (= núcleo) no puede vibrar sin ser expuesta a tensión (= campo magnético externo). Cuanta más alta es la tensión, mayor será la frecuencia de vibración.
En ambos ejemplos, se han hecho comparaciones entre un sistema nuclear macroscópico y uno microscópico. En el primer ejemplo hemos comparado los núcleos atómicos con pequeñas agujas magnéticas y en el segundo con cuerdas de guitarra.
Dichos paralelismos proporcionan una imagen mental del fenómeno pero tienen sus inconvenientes. Una de las limitaciones de estos modelos es que todos los fenómenos físicos a escala molecular son de tipo cuántico. Por ejemplo, mientras la aguja magnética podría situarse en una infinidad de orientaciones diferentes, no existen suaves transiciones continuas entre el estado de equilibrio y el estado inestable rico en energía en el caso del núcleo magnético; la mecánica cuántica predice que sólo son posibles los saltos entre estos dos estados en núcleos con un espín de ½, tales como los protones (Figura 02-06) [espín de ½: ⇒ Holland 1993].
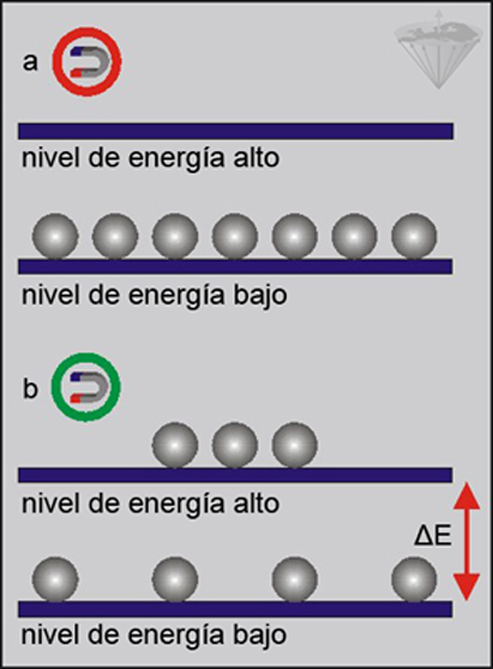
Figura 02-06:
(a) Protones fuera de un campo magnético y
(b) protones dentro de un campo magnético.
En presencia de un campo magnético, los núcleos poblarán dos niveles de energía distintos. La separación entre estos niveles aumenta linealmente con la fuerza del campo magnético, así como también la diferencia de población.
En equilibrio observamos una población ligeramente mayor en el nivel de energía más bajo, produciéndose así una magnetización neta. Para observar esta diferencia de población tenemos que transmitir una cantidad de energía igual a ΔE (la diferencia de energía entre los dos niveles).
|
|
|---|